Код на холограмата, бутилката на Клайн
Мечтата на средновековния алхимик е мистичен съвършен херметичен съд, където външното преминава във вътрешно и вътрешното – във външно, който съдържа сам себе си и преминава сам в себе си, при който вътрешното и външното са парадоксално едно…
Всичко това напомня змия, уроборос, захапал опашката си.
Оказва се, че съществува такъв парадоксален обект и това е бутилката на Клайн.

Портрет на Феликс Клайн. © Max Liebermann, Mathematischen Institut der Universität Göttingen
Първото споменаване за нея се появило през 1882 г., а автор бил немският математик Феликс Клайн (Felix Klein), създател на ново направление в геометрията. Клайн е роден на 25 април 1849 година.
Първото название на бутилката на Клайн е „Klein Fla-e-che“ (Fläche = повърхност), повърхност на Клайн. Но в названието думата Fläche била интерпретирана като Fla-s-che (бутилка) и поради доминирането на английския език се утвърдило в математическата наука, а по-късно терминът „бутилка на Клайн“ също влязъл в употреба в Германия.
Векове думата „геометрия“ се употребявала в единствено число. Но ето че се появила геометрия на Лобачевски, след това – геометрия на Риман и накрая математиците разбрали, че съществуват много различни геометрии.
Възникнал и естественият въпрос: какво е геометрия? През 1872 година Клайн изказал своята гледна точка на лекции, четени от него във връзка с встъпването му в професорска длъжност в Ерланген. Така се появила „Ерлангенската програма“. Тя привличала вниманието на математиците от цяла Европа с това, че не само давала нова представа за предмета геометрия, но и набелязвала ясна перспектива за бъдещи изследвания.
С това да приключим обяснителната част и да преминем към нещо по-интересно, свързано с името на Клайн – бутилката на Клайн.
От гледна точка на математиката бутилката на Клайн е затворена едностранна повърхност.
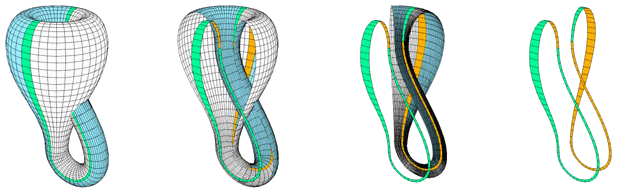
А от гледна точка на физиката? Как да си представим на какво прилича поразителната бутилка в реалността?
Да допуснем, че имаме бутилка с много дълго гърло, в стената и в дъното на бутилката има отвори, съответстващи на размера на гърлото. Вземаме бутилката за гърлото, огъваме го, пъхваме го през страничния отвор и го изтегляме до отвора в дъното на бутилката, след което ги залепяме. Ето че се получи!
Къде е началото и къде – краят, е невъзможно да се каже…
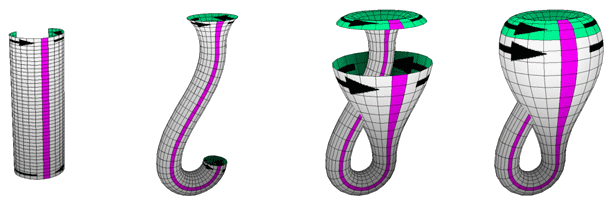
Такава бутилка няма край и нейната повърхност не може да се раздели на външна и вътрешна.
Помните ли листа на Мьобиус и пълзящата по него мравка? Пътешествието на тази мравка по повърхността на бутилката на Клайн също се превръща в безкрайност. Няма да ѝ се налага да преминава от външната страна на бутилката във вътрешната – тя е единствена. Истинската бутилка на Клайн в четириизмерно пространство не се пресича сама със себе си.


Да допуснем, че имаме бутилка с много дълго гърло, в стената и в дъното на бутилката има отвори, съответстващи на размера на гърлото. Вземаме бутилката за гърлото, огъваме го, пъхваме го през страничния отвор и го изтегляме до отвора в дъното на бутилката, след което ги залепяме. Ето че се получи!
Къде е началото и къде – краят, е невъзможно да се каже…

Такава бутилка няма край и нейната повърхност не може да се раздели на външна и вътрешна.
Помните ли листа на Мьобиус и пълзящата по него мравка? Пътешествието на тази мравка по повърхността на бутилката на Клайн също се превръща в безкрайност. Няма да ѝ се налага да преминава от външната страна на бутилката във вътрешната – тя е единствена. Истинската бутилка на Клайн в четириизмерно пространство не се пресича сама със себе си.


За разлика от реалните бутилки повърхността на бутилката на Клайн няма граници, където да се прекъсва. За разлика от топка или тор мухата, пълзяща по повърхността на бутилката на Клайн, може да попадне от външната страна във вътрешната, без за преминава през повърхността.
Ако разделим бутилката по вертикалната симетрична ос, то ще получим два листа на Мьобиус.
Ако разделим бутилката по вертикалната симетрична ос, то ще получим два листа на Мьобиус.
Но е интересно, че с един затворен разрез бутилката на Клайн може да се превърне само в един лист на Мьобиус.
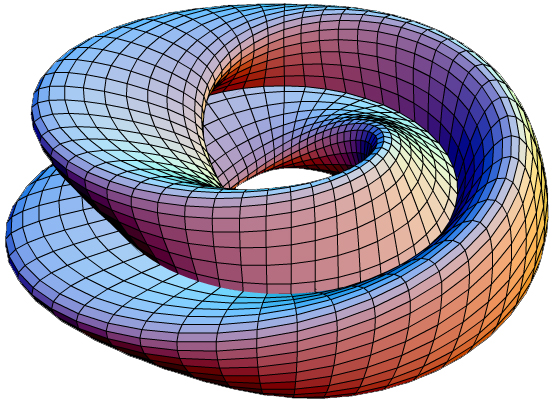
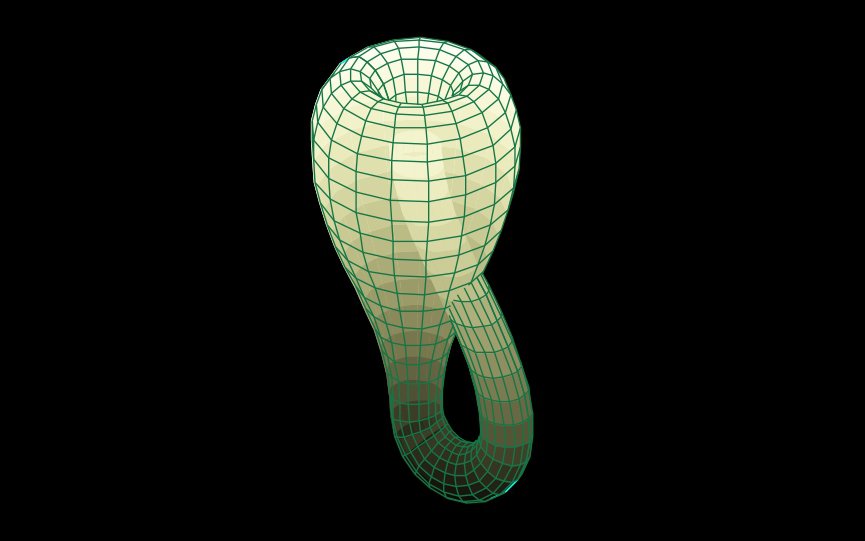
А ето нагледен 3D модел на бутилката на Клайн.
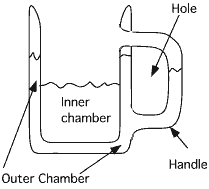
Диаграма показва напречно сечение през чаша за пиене на бира - халбата на Клайн - с един единствен отвор,
Евклидовата геометрия научихме в училище.
Псевдо-евклидовата геометрия научаваме чрез изучаване на специална теория на относителността на Айнщайн.
Но нашият свят е още по-сложен, следващата стъпка е да се опитаме да овладеем неевклидовата геометрия.
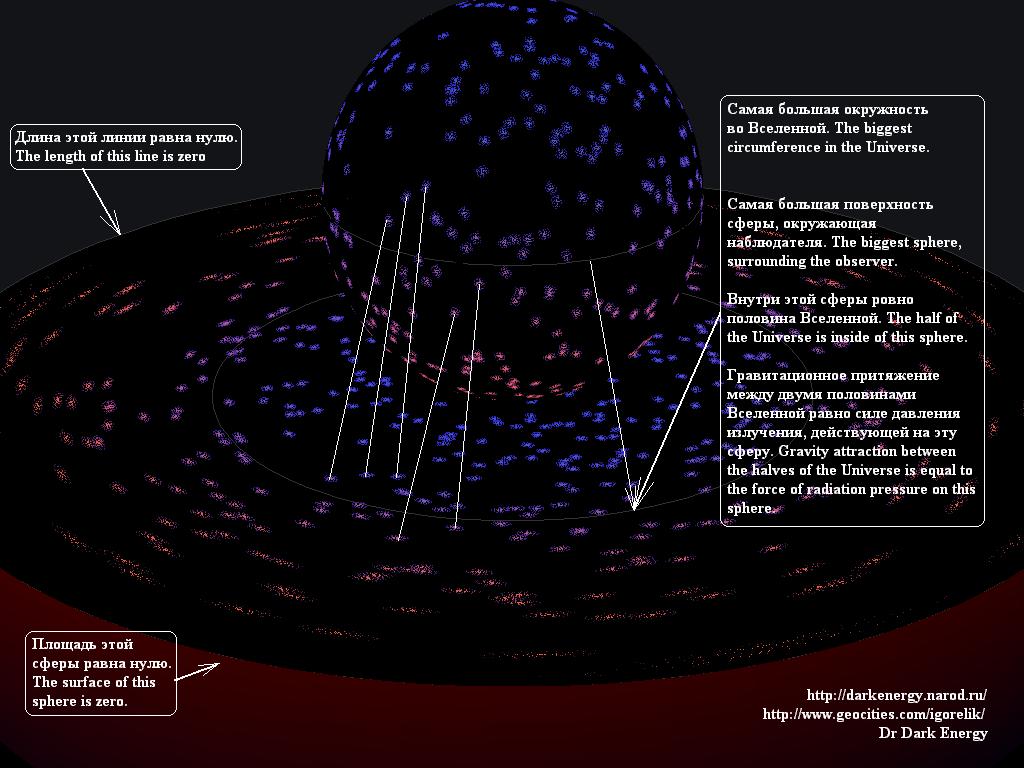
На следващата снимка можете да видите пример за неевклидова геометрия. Попитах приятелите ми какво е то. Отговорите бяха, както следва: на TARDIS, бутилка Klein, входа на черната дупка, НЛО, машина на времето, конвертор на размер, конвертор на пространство. Какво е това, ако тя може да бъде точно същата секунда колата, вътре втората кола може да бъде една трета, в третата в първата кола - четвъртият ... И в някоя от тези машини, можем да получим чрез промяна на техните размери.
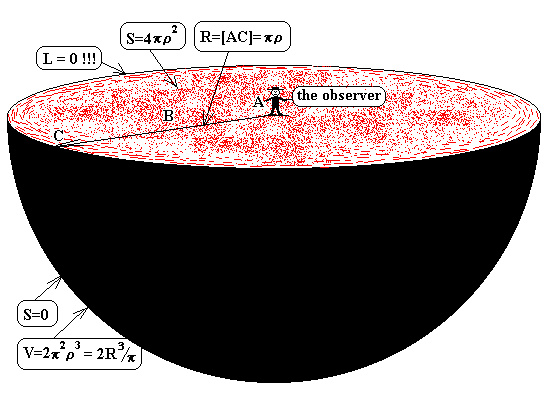
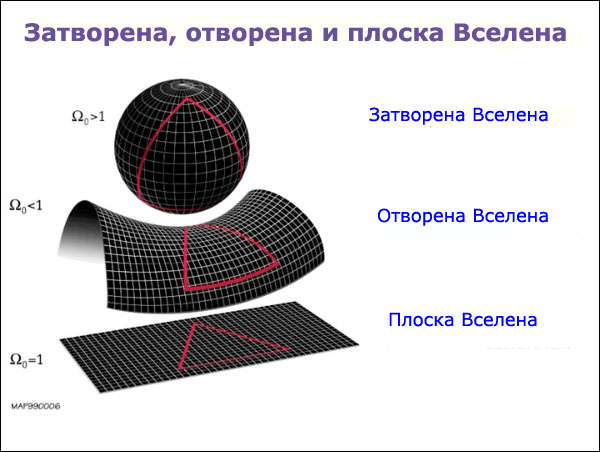
Между другото, снимката не е толкова фантастична. Има някои идеи за практическото прилагане на TARDIS, или интервал конвертор. Нещо повече, той вече съществува - вселената на пространство-времето може да има свойства, подобни на тези, показани на фигурата. Вселената като цяло е вероятно да има положителна кривина, и на местно ниво някои огромни междугалактически облаци прах може да даде неравенството: D <г, където D - външен диаметър на сферичната слой, г - вътрешен диаметър на сферичната обвивка. В евклидовата геометрия са известни D = г + 2а, където дебелина е "а" стена. Подобно неравенство може да се запише за галактическите клетки във Вселената, в която стената представя различни галактики, и в стотици празнота. И за цялата вселена на неговия външен диаметър D е равно на нула. Виж. Раздел на затворена вселена , както и компютърна графика вселена
Бутилката на Клайн - играчка за математици
На следващата снимка можете да видите пример за неевклидова геометрия. Попитах приятелите ми какво е то. Отговорите бяха, както следва: на TARDIS, бутилка Klein, входа на черната дупка, НЛО, машина на времето, конвертор на размер, конвертор на пространство. Какво е това, ако тя може да бъде точно същата секунда колата, вътре втората кола може да бъде една трета, в третата в първата кола - четвъртият ... И в някоя от тези машини, можем да получим чрез промяна на техните размери.
http://darkenergy.narod.ru/4dru.html
Ако търсите къде да си налеете питие, една бутилка на Клайн няма да ви свърши работа. Тя може да ви напомня на бутилка, но няма никакъв обем, което означава, че каквото и да се налива "вътре", ще се окаже навън.
Как да се направи такова странно нещо и защо ни трябва?
Математикът Феликс Клайн , който е открил бутилката през 1882 г., я описва като повърхност, която "може да се визуализира като се обърне парче гумена тръба и да направим възможно да премине през себе си, така че вътрешната и външната повърхности да се срещнат". Бутилката на Клайн е в галерията на най-популярните математически форми, известни на широката публика.
Бутилката на Клайн се образува като се съединят двете страни на лист, за да стане цилиндър (тръба), а след това се извиват краищата на цилиндъра обратно през самия него по такъв начин, че вътрешната страна (в зелено) и външната (в бяло) на цилиндъра се съединяват. Анимация от Konrad Polthier.
Очевидно е, че бутилката на Клайн, точно като по-познатата ни сфера, е затворена повърхност: тя е ограничена, в смисъл, че може да се вмести в ограничена област на пространството. Една мравка може да се разхожда по нея вечно, без изобщо да се натъкне на граница или да падне от някой ръб. За разлика от сферата, която има вътрешна и външна повърхност, бутилката на Клайн обаче има една страна: разхождайки се нашата мравка може да достигне до двете страни на всяка точка от повърхността.
Бутилката не обхваща обем и нищо не можем да налеем "вътре", защото няма "вътре" или "вън" - повърхността е една.
А това прави бутилката на Клайн е интересна, защото не се срещат често едностранни форми в природата.
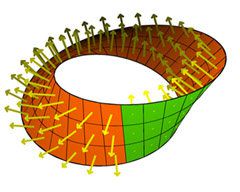

Мьобиусовата лента е едностранна. Схема и анимация: Konrad Polthier.
Ако бутилката е малко объркваща, има един по-прост пример за едностранна повърхност: известният Мьобиусов лист. Можете да направите един, като обърнете един от двата края на лента от хартия и го залепите на другия край. С помощта на хартиена лента, чиито две страни имат различни цветове, да кажем, зелено и оранжево, лесно ще се убедите, че Мьобиусовата лента е едностранна. След като сте усукали краищата и залепили, ще откриете, че може да стигнете до всяка оранжева и всяка зелена точка, без да се налага да пробивате хартията или да се катерите през ръба й.
За разлика от бутилката на Клайн, лентата на Мьобиус има край, има граница - тя се състои от двата отделни слепени краища на оригиналната лента. Но двата края са свързани. Границата на лентата на Мьобиус е единична затворена крива.
Ако имаме две Мьобиусови ленти за да се създаде една затворена форма, като се присъединят техните граници с помощта на обикновена двустранна лента, както е показано по-долу, а това, което се получава е точно бутилката на Клайн.
Двете Мьобиусови ленти се свръзват в бутилка на Клайн чрез обикновена двустранна лента, чиято задна и предна повърхност са оцветени в бяло и синьо, съответно. Анимация от Konrad Polthier.
Друга любопитна особеност на бутилката на Клайн е, че сама се пресича, което означава, че е трудно да се направи от една каучукова тръба както предлага Клайн. Строго погледнато, самопресичащите се обекти показани по-горе, не са бутилка на Клайн, но както посочва Клайн, тя е само въображаем обект в нашето 3D пространство. Но може да бъде успешно конструирана в 4D пространството, без самопресичане и дупка в повърхнината.
За да разберем защо, първо да разгледаме добре познатия геврек или пояс (известен на математиците като тор). Може да направим тор от квадратен лист от каучук, като първо залепим двете срещуположни страни като цилиндър, а след това залепваме двата края на цилиндъра за да получим тор.

Построяване на тор: Първо залепваме противоположните точки на две противоположни страни на квадрата, за да се направи цилиндър и след това залепете двата гранични кръга на цилиндъра съответстващи на залепване противоположни точки на останалите две страни на квадрата за да образуваме тор.
Ако не искате да се занимавате с лепене, можете просто да си представите тора като квадрат като имате предвид, че противоположните точки на противоположните страни се смятат за едни и същи. Така че, когато се плъзга някаква фигура, нарисувана върху "квадрата", към горния ръб, тя ще се появи отново в долния край, а когато я плъзнете към десния край ще се появи отново в левия ръб и обратно.
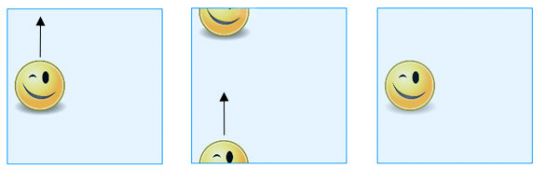
Когато плъзнете фигура нарисувана върху "квадрата" към горния ръб, тя ще се появи отново в долния край.
За да получите истинска бутилка на Клайн, започнете по същия начин като намерите противоположните точки на двойката противоположни страни на квадрата. За другата двойка страни, обаче, не се идентифицират точки, които са пряко противоположни, а точки, които са по диагонал, както е показано на снимката.
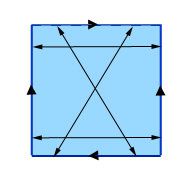
Построяване на бутилка на Клайн: съединявват се противоположните точки на две противоположни страни (вертикалните в тази схема), а след това се съединявват диагонално противоположните точки на останалите две страни. Ако квадраттът е [0,1] × [0,1] отъждествяваме точките (x, -1) с (-x, 1) и (-1, y) с (1, y) . Така отъждествяването на страните на квадрата по x става „с усукване“, а по y - „без усукване“.
Полученият обект е бутилката Клайн. Отново може да си я представите като квадрат като имате предвид кои гранични точки се смятат за едни и същи. Ако плъзнете фигурата над един от ръбовете, които имат противоположни точки (вертикалните страни в нашия случай), тя се появява отново на противоположната страна, като преди. Ако обаче я плъзнете над един от ръбовете, чиито точки са били идентифицирани по диагонал (хоризонталните страни), тя се появява на противоположната страна, но изместена и като огледален образ на оригиналния си.
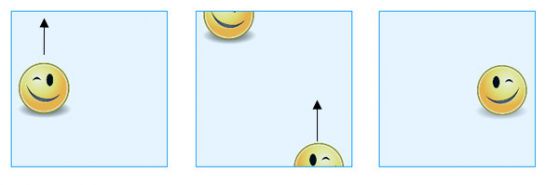
Ако плъзнете форма над горния край, тя се появява през долния ръб от другата страна и като огледален образ на оригиналния си.
Единственият начин да се изгради тази форма в триизмерното пространство е да се даде възможност тя да се пресича. Това се равнява на идентифициране на двойки от точки във вътрешността на оригиналния квадрат, така че строго погледнато получената фигура не е точно същата като бутилката на Клайни. Това е просто един начин за представяне на бутилката в триизмерното пространство (има и други).
Ориентируемост и едностранност
Най-важните свойства на лентата на Мьобиус и бутилката на Клайн са тяхната ориентируемост и едностранност. Една повърхност е едностранна, ако може да се разходите прав по повърхността като стигнете до двете страни на всяка точка от повърхността. Повечето повърхности в природата са двустранни . Например, кръгла сфера е двустранна, което е гаранция, че винаги ще ходим върху Земята и никога с глава в скалите. По същия начин и по повърхността на тора (геврека) и въобще по всички повърхности, които покриват твърд обем, са двустранни.
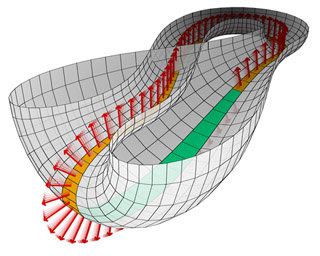

В природата не може да се видят едностранни повърхнини. Първата едностранна повърхност, открита от Мьобиус, е абстрактно математическо построение. Перпендикулярните стрелички (по математически - нормални вектори ), които видяхме по-горе върху лентата на Мьобиус, в горната илюстрация на бутилката на Клайн показват нейната едностранност: непрекъснато движейки се, стреличките обхождат двете страни на повърхността на една точка, което означава, че няма разлика между горно и долно (предно и задно, вътре и вън).
Любопитното е, че понятията за "вътре", "отвън" и "едностранчивост" зависят от околното пространство, в което обектът се намира. Например, една затворена крива (контур), нарисувана върху лист хартия (т.е. в двумерното пространство) има добре дефинирани "вътре" и "отвън", то при същият контур, поставен в тримерното пространство, тези понятия губят смисъл. Ето защо не можем да говорим за едностранчивост, освен ако първо не се определи как се вгражда тази повърхнина в пространството. Има обаче по-тясно свързани свойства, присъщи на една повърхнината, които не зависят от околното пространство.
За една повърхност се казва, че е ориентируема, ако фигура, нарисувана върху нея, не може да се трансформира в своя огледален образ, колкото и да се плъзга по повърхността.
Ориентируемост. Анимация от Konrad Polthier
Както можете да видите в анимацията горе, ако придвижите изображението на лице около лентата на Мьобиус, то се завръща като своя огледален образ ( с главата надолу). Това означава, че лентата на Мьобиус е неориентируема. А от примера с плъзгащото се усмихнато лице по-горе, се вижда, че и бутилката на Клайн не е ориентируема.
Понятието ориентируемост важи и за тримерни пространства. Например в една неориентируема тримерна вселена можем така да подхвърлим дясната си ръкавица, че да се върне като лява ръкавица!
Ако трябва да отговорим на въпроса в заглавието - да, може да се напълни в нашия тримерен свят бутилка на Клайн, но е много трудно. Течността създава допълнително налягане върху въздуха вътре, а той няма къде да се измъкне. И изливането на течността е проблем. Освен това течността в бутилката на Клайн не се изпарява, а и да се почистят стените отвътре е практически невъзможно. Но така или иначе, математиците не я ценят заради качествата й на сервиз за вино.
Началото на всички начала, или Големият взрив, е съпровождано не само от материя, но и от лъчение. И това електромагнитно лъчение, наречено реликтово, има свои, неизменни физически характеристики, които позволяват на астрофизиците да го отличават от обширната разновидност на другите „космически лъчи“. Смята се, че реликтовото лъчение и до днес равномерно изпълва Вселената. Експериментално неговото съществуване е било потвърдено още през 1965 г.
Сама в себе си?
Изследвайки реликтовото лъчение, съветският учен Д. Иваненко още в средата на миналия век изказал предположението, че Вселената, първо, е затворена, а второ, далеч не навсякъде се подчинява на законите на Евклидовата геометрия.
Неподчинението на Евклидовата геометрия означава, че има места, където успоредните линии се пресичат и дори се сливат една с друга. Затвореността на Вселената означава, че тя, възможно, е затворена „сама в себе си“. Отправяйки се на пътешествие от една нейна точка (да речем – планетата Земя) и движейки се, както ни се струва, строго по права линия, ние в края на краищата ще се озовем на същото място, на Земята – макар и след много години.
Косвено потвърждение на теорията на Иваненко и неговите последователи е получено през 2001 година. Американската сонда WMAP (Wilkinson Microwave Anisotropy Probe) предава на Земята данни за флуктуации (изменения, колебания) на температурите на реликтовото лъчение. Астрофизиците се заинтересували от размерите и характера на разпределение на тези флуктуации. Било проведено компютърно моделиране, показващо, че подобен характер на флуктуациите може да се наблюдава само в случай че Вселената е ограничена и затворена сама в себе си.
Законите са еднакви навсякъде
Дори лъчът светлина, разпространявайки се в пространството, след определен (голям) период от време трябва да се върне в изходната точка. Значи астрономите от Земята могат например да наблюдават една и съща галактика в различни части на небосвода, пък и от различни страни!

© GuidoJ
Ако данните от WMAP бъдат потвърдени, нашите възгледи за Вселената ще се променят много силно. Първо, тя ще се окаже сравнително малка – простираща се на не повече от 10 милиарда години
Второ, нейната форма може да се окаже тор (геврек) а това е нещо съвсем екзотично, например бутилка на Клайн. А и това ще означава, че ние можем да наблюдаваме цялата Вселена и да се убедим, че навсякъде действат едни и същи физични закони.
http://megavselena.bg/vselenata-v-butilka/
Върху сфера сборът от трите ъгъла на триъгълник не е равен на 180°. Сферичната повърхнина не е евклидово пространство, но локално твърденията на евклидовата геометрия са добра апроксимация. В малки триъгълници от повърхнината на Земята сборът от ъглите е близък до 180°.
Какво представлява пространство-време с отрицателна кривина
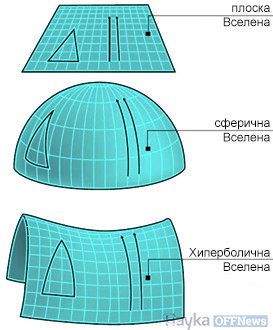
В добре познатата ни евклидова геометрия пространството е плоско, т.е. не е изкривено. До известна степен това е вярно за света около нас: успоредните линии никога не се пресичат и се изпълняват всички други аксиоми на Евклид.
Имаме представа и какво е изкривено пространство. Кривината може да бъде положителна или отрицателна. Най-простото пространство с положителна кривина е повърхността на сфера, която има постоянна положителна кривина, т.е. еднакво е изкривена във всяка точка - яйцето например няма постоянна кривина.
Най-простото пространство с постоянна отрицателна кривина е хиперболичното. В една от картините си Ешер е изобразил плоска карта на такова пространство. По краищата на рибките стават все по-малки, заради това, че изкривеното пространство се деформира, когато се показва на плосък лист хартия. По същия начин, в географските карти на света площите близо до полюсите са разтегнати.

Може да се разглежда и пространство-време с положителна или отрицателна кривина. Най-простото пространство-време с положителна кривина се нарича пространство де Ситер в чест на холандския физик Вилем де Ситер, който го въвежда. Много космолози смятат, че най-ранната Вселена е била подобна до пространството де Ситер. Но в по-далечно бъдеще, поради космическото ускорение, тя може отново да стане като него.
Най-простото пространство-време с отрицателна кривина се нарича пространство анти-де Ситер (или съкратено - AdS - пространство). То е подобно на хиперболичното, но има и ос време. За разлика от нашата Вселена, която се разширява AdS - пространството не се разширява и не се свива, а винаги изглежда по един и същи начин. Въпреки това, то е много полезно при разработването квантови теории на пространство-времето и гравитацията.
Имаме представа и какво е изкривено пространство. Кривината може да бъде положителна или отрицателна. Най-простото пространство с положителна кривина е повърхността на сфера, която има постоянна положителна кривина, т.е. еднакво е изкривена във всяка точка - яйцето например няма постоянна кривина.
Най-простото пространство с постоянна отрицателна кривина е хиперболичното. В една от картините си Ешер е изобразил плоска карта на такова пространство. По краищата на рибките стават все по-малки, заради това, че изкривеното пространство се деформира, когато се показва на плосък лист хартия. По същия начин, в географските карти на света площите близо до полюсите са разтегнати.

Може да се разглежда и пространство-време с положителна или отрицателна кривина. Най-простото пространство-време с положителна кривина се нарича пространство де Ситер в чест на холандския физик Вилем де Ситер, който го въвежда. Много космолози смятат, че най-ранната Вселена е била подобна до пространството де Ситер. Но в по-далечно бъдеще, поради космическото ускорение, тя може отново да стане като него.
Най-простото пространство-време с отрицателна кривина се нарича пространство анти-де Ситер (или съкратено - AdS - пространство). То е подобно на хиперболичното, но има и ос време. За разлика от нашата Вселена, която се разширява AdS - пространството не се разширява и не се свива, а винаги изглежда по един и същи начин. Въпреки това, то е много полезно при разработването квантови теории на пространство-времето и гравитацията.


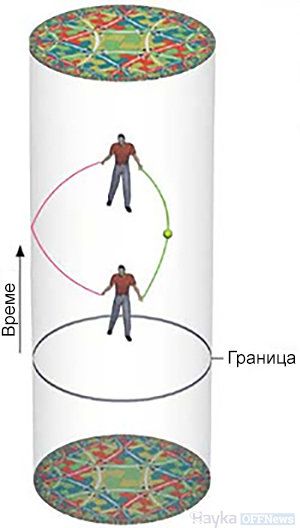
Ако сe изобрази хиперболичното пространство като диск, напомнящ рисунката на Ешер, това AdS - пространството ще бъде подобно купчина от дискове, образуващ твърд цилиндър. Изменението по оста на времето съответства на движение по дължината на цилиндъра. Хиперболичното пространство може да има повече от две измерения. AdS - пространството прилича много на нашето пространство-време (с три пространствени измерения) и дава в напречното сечение на своя "цилиндър" триизмерна картина на Ешер.
Физика в AdS - пространството е малко необичайна. Ако един наблюдател се придвижва свободно, би се чувствал като на дъното на гравитационен кладенец. Всеки хвърлен от него обект, би се връщал обратно към него като бумеранг. Любопитното е, че времето, необходимо за връщане, няма да зависи от силата, с която обекта е хвърлен. Но колкото по-силно е хвърлен, толкова по-далече ще лети.
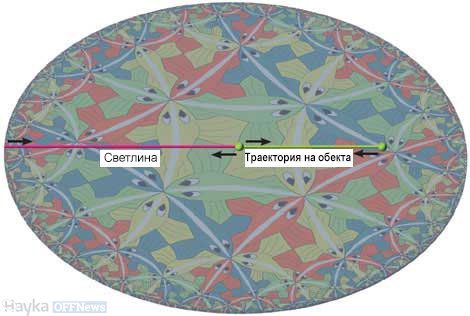
Ако някой в AdS - пространството изпрати лъч нанякъде, фотоните, които се движат със скоростта на светлината ще достигнат безкрайност и ще се върнат към източника за крайно време. Лазерният лъч (червена линия) ще достигне границата на вселената и ще се върне за едно и също време. В четиримерното AdS - пространство, което прилича на нашата Вселена, границата във всеки момент няма да е кръг и сфера.
Работата е там, че обектите в AdS - пространството, отдалечавайки се от наблюдателя, ще изпитват свиване на времето.
Холограма
Безкрайното AdS - пространство е оградено от безкрайната граница. За да се изобрази тя, физиците и математиците използват изкривен мащаб на дължините, който позволява да се компресира безкрайно разстояние в крайно. Споменатата граница е подобна на външната обиколка на картината на Ешер, или на повърхността на плътния цилиндър, разгледан по-горе. В последния случай границата има две измерения: пространствено (управителна крива на цилиндъра) и времето (образуващата цилиндъра). Границата на четиримерното AdS - пространство-времето има две пространствени измерения и едно времево. Във всеки момент време тя е сфера, на която е разположена холограмата, разглеждана в холограмната теория.
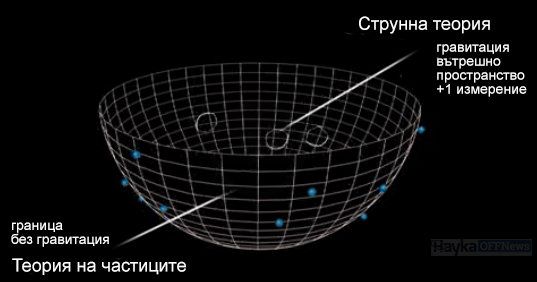
Холограмната теория съпоставя едни физически закони, които действат в определен обем, с други, които важат за повърхността, която го огражда. Физиката на границата е представена от квантови частици, които имат "цветни" заряди и си взаимодействат почти като кварките и глуоните в стандартната физика на елементарните частици. Законите вътре са разновидност на теорията на струните, включително гравитацията, която трудно може да се опише от гледна точка на квантовата механика. Но физиката на повърхността и физиката в обема са напълно еквивалентни въпреки различните начини за описание.
Идеята е следната: квантовата теория на гравитацията в AdS-пространство-времето е напълно еквивалентна на обикновената квантова теория на частиците, намиращи се на границата. Еквивалентността означава, че може да се използва сравнително ясната квантовата теория на частиците, за да се създаде все още неясната квантова теория на гравитацията.
Представете си две копия на един филм, единият - на лента, а другият - на DVD. В първия случай ако разгледаме целулоидна кинолента лесно можем всеки кадър да свържем с определен епизод от филма. Във втория случай имаме диск с пръстени от точки, които отразяват по различен начин лазерната светлина, за да образуват поредица от нули и единици, които не могат да предизвикат някакъв образ в съзнанието ни. Независимо от това и двата носителя описват един и същи филм.
По същия начин двете теории, на пръв поглед, съвсем различни по съдържание, описват една и съща Вселена. DVD наподобява дъга блестящ метален диск, а теорията на частиците на границата на "напомня" теория на частици без гравитацията. Кадрите на филма, записан на DVD, се появяват на екрана само след съответна обработка на битовете. Квантовата гравитация и допълнително измерение се проявяват от теорията на частиците на границата само тогава, когато нейните уравнения правилно са анализирани.
Физика в AdS - пространството е малко необичайна. Ако един наблюдател се придвижва свободно, би се чувствал като на дъното на гравитационен кладенец. Всеки хвърлен от него обект, би се връщал обратно към него като бумеранг. Любопитното е, че времето, необходимо за връщане, няма да зависи от силата, с която обекта е хвърлен. Но колкото по-силно е хвърлен, толкова по-далече ще лети.
Ако някой в AdS - пространството изпрати лъч нанякъде, фотоните, които се движат със скоростта на светлината ще достигнат безкрайност и ще се върнат към източника за крайно време. Лазерният лъч (червена линия) ще достигне границата на вселената и ще се върне за едно и също време. В четиримерното AdS - пространство, което прилича на нашата Вселена, границата във всеки момент няма да е кръг и сфера.
Работата е там, че обектите в AdS - пространството, отдалечавайки се от наблюдателя, ще изпитват свиване на времето.
Холограма
Безкрайното AdS - пространство е оградено от безкрайната граница. За да се изобрази тя, физиците и математиците използват изкривен мащаб на дължините, който позволява да се компресира безкрайно разстояние в крайно. Споменатата граница е подобна на външната обиколка на картината на Ешер, или на повърхността на плътния цилиндър, разгледан по-горе. В последния случай границата има две измерения: пространствено (управителна крива на цилиндъра) и времето (образуващата цилиндъра). Границата на четиримерното AdS - пространство-времето има две пространствени измерения и едно времево. Във всеки момент време тя е сфера, на която е разположена холограмата, разглеждана в холограмната теория.
Холограмната теория съпоставя едни физически закони, които действат в определен обем, с други, които важат за повърхността, която го огражда. Физиката на границата е представена от квантови частици, които имат "цветни" заряди и си взаимодействат почти като кварките и глуоните в стандартната физика на елементарните частици. Законите вътре са разновидност на теорията на струните, включително гравитацията, която трудно може да се опише от гледна точка на квантовата механика. Но физиката на повърхността и физиката в обема са напълно еквивалентни въпреки различните начини за описание.
Идеята е следната: квантовата теория на гравитацията в AdS-пространство-времето е напълно еквивалентна на обикновената квантова теория на частиците, намиращи се на границата. Еквивалентността означава, че може да се използва сравнително ясната квантовата теория на частиците, за да се създаде все още неясната квантова теория на гравитацията.
Представете си две копия на един филм, единият - на лента, а другият - на DVD. В първия случай ако разгледаме целулоидна кинолента лесно можем всеки кадър да свържем с определен епизод от филма. Във втория случай имаме диск с пръстени от точки, които отразяват по различен начин лазерната светлина, за да образуват поредица от нули и единици, които не могат да предизвикат някакъв образ в съзнанието ни. Независимо от това и двата носителя описват един и същи филм.
По същия начин двете теории, на пръв поглед, съвсем различни по съдържание, описват една и съща Вселена. DVD наподобява дъга блестящ метален диск, а теорията на частиците на границата на "напомня" теория на частици без гравитацията. Кадрите на филма, записан на DVD, се появяват на екрана само след съответна обработка на битовете. Квантовата гравитация и допълнително измерение се проявяват от теорията на частиците на границата само тогава, когато нейните уравнения правилно са анализирани.

Какво означава две теории да са еквивалентни? Първо, за всеки обект в едната теория трябва да съществува аналог в другата. Описанията на обектите могат да бъдат доста различни: на определена частица вътре в пространството може да съответства цял набор от частици на границата, разглеждан като едно цяло. Второ, прогнозата за съответните обекти да бъдат едни и същи. Например, ако две частици се сблъскват в пространството с вероятност 40%, то съответният набор от частици на границата трябва да се сблъсква също с вероятност 40%.
Да разгледаме еквивалентността по-подробно. Взаимодействията на частиците, които съществуват на границата са много подобни на взаимодействията на кварките и глуоните (кварките съставят протоните и неутрони, а глуоните създават силното ядрено взаимодействие, което свързва кварките). Кварките имат нещо като заряд като различните му видове се наричат цветове, а законите на тяхното взаимодействие - хромодинамика. За разлика от обикновените кварки и глуони, частиците на границата имат не три, но много по-голям брой цветове.
Герард'т Хоофт (Gerard't Hooft ) от Университета в Утрехт в Холандия се е занимавал с подобни теории още през 1974 г. и прогнозира, че глуоните могат са образуват вериги, които да се държат почти като струните в струнната теория. Техният характер остава неясен, но през 1981 г., Александър Поляков, който сега работи в Принстънския университет, забелязал, че пространството, в което съществуват струните, имат повече измерения от това, в което съществуват глуоните. В холограмните теории пространство с повече измерения е вътрешната част на AdS - пространство.
Магията на измеренията
Холограмната теория описва как кварките и глуоните взаимодействат на границата на AdS - пространството могат да бъдат еквивалентни на частици във вътрешната му област с повече измерения.
Кварките и глуоните в сферичната повърхност на AdS - пространството взаимодействат, образувайки струни с различна дебелина. Според холограмната интерпретация във вътрешното пространство, тези струни са представени от елементарни частици (които също са струни), разположени на известно разстояние от границата, което зависи от дебелината на струната.
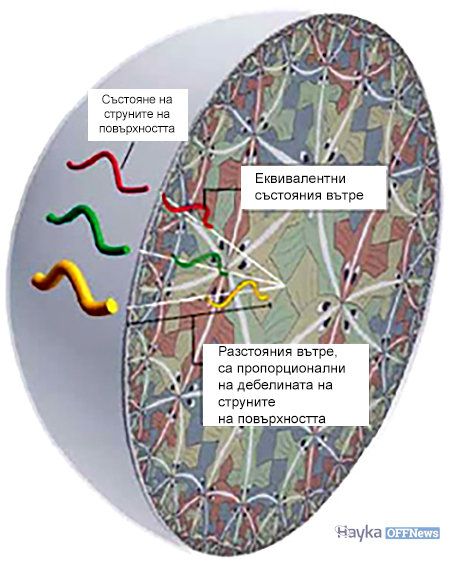
Така облакът от кварки и глуони на граничната повърхност могат да описват еквивалентно сложни обекти (като тази ябълка) вътре в обема. Предимството на холограмната теория е, че вътрешните обекти изпитват гравитация, макар гравитационното взаимодействие на границата просто не съществува

За да разберем, от къде се появяват допълнителното измерение, да разгледаме една от глуонните струни на границата. Струната има дебелина, която зависи от това, доколко глуоните са размазани в пространството. Изчисленията показват, че в границата на AdS - пространството струните с различни дебелини взаимодействат една с друга толкова слабо, като че ли са разделени в пространството. С други думи, дебелината на струните може да се разглежда като пространствена координата, ос която е насочена от границата.
Така, тънката гранична струна прилича на струна, която се намира близо до границата, докато дебелата струна прилича на отдалечена от границата струна. Именно тази допълнителна координата е нужна за да се опише движението в четиримерното AdS-пространство-време! За наблюдателят в пространствено-времето граничните струни с различна дебелина изглеждат еднакво тънки, но с различни радиални позиции. Броят на цветовете на границата се определя от размера на вътрешната част на пространството (радиуса на граничната сфера). За да не отстъпва на пространство-времето по размери на видимата Вселена, на теория трябва да бъде с не по-малко от 1060 цвята.
Оказва се, че един тип глуонна верига се държи в четиримерното пространство-време, като гравитон, фундаменталната квантова частица на гравитацията. В това описание, гравитацията в четири измерения е явление, възникващо в резултат от взаимодействието на частици в тримерен свят без гравитация. Появата в теорията на гравитоните не е изненада, защото физиците знаят от 1974 г. насам, че теорията на струните по един или друг начин ще доведе до квантовата гравитация. Струните, образувани от глуони не са изключение, просто гравитацията работи в пространство с повече измерения.
Така холограмното съответствие е не просто нова възможност за създаване на квантовата теория на гравитацията. То по фундаментален начин обединява струнната теория като най-изучен подход към квантовата гравитация с теорията на кварките и глуоните, която е в основата на физиката на елементарните частици. Освен това, холограмната теория, очевидно, позволява да се състави някаква представа за точните уравнения на теорията на струните. Тя е измислена в края на 1960, за да опише силните взаимодействия, но е изоставена, когато на сцената се в появила теорията на хромодинамиката. Съответствието между струнната теория и хромодинамиката предполага, че последните усилия не са били напразни. Двете описания са различни страни на една и съща монета
Като варира хромодинамиката на границата, т.е. променя детайлите на взаимодействието на граничните частици може да се получи цял спектър от теории. По принцип на вътрешното пространство може да съдържа само гравитационната сила или гравитацията и други сили, например, електромагнитната и т.н. Все още предстои да се разработи такава гранична теория, от която то да бъде възможно да се изведе описание на вътрешното пространство, съдържащо четирите сили, управляващи нашата Вселена.
Да разгледаме еквивалентността по-подробно. Взаимодействията на частиците, които съществуват на границата са много подобни на взаимодействията на кварките и глуоните (кварките съставят протоните и неутрони, а глуоните създават силното ядрено взаимодействие, което свързва кварките). Кварките имат нещо като заряд като различните му видове се наричат цветове, а законите на тяхното взаимодействие - хромодинамика. За разлика от обикновените кварки и глуони, частиците на границата имат не три, но много по-голям брой цветове.
Герард'т Хоофт (Gerard't Hooft ) от Университета в Утрехт в Холандия се е занимавал с подобни теории още през 1974 г. и прогнозира, че глуоните могат са образуват вериги, които да се държат почти като струните в струнната теория. Техният характер остава неясен, но през 1981 г., Александър Поляков, който сега работи в Принстънския университет, забелязал, че пространството, в което съществуват струните, имат повече измерения от това, в което съществуват глуоните. В холограмните теории пространство с повече измерения е вътрешната част на AdS - пространство.
Магията на измеренията
Холограмната теория описва как кварките и глуоните взаимодействат на границата на AdS - пространството могат да бъдат еквивалентни на частици във вътрешната му област с повече измерения.
Кварките и глуоните в сферичната повърхност на AdS - пространството взаимодействат, образувайки струни с различна дебелина. Според холограмната интерпретация във вътрешното пространство, тези струни са представени от елементарни частици (които също са струни), разположени на известно разстояние от границата, което зависи от дебелината на струната.

Така облакът от кварки и глуони на граничната повърхност могат да описват еквивалентно сложни обекти (като тази ябълка) вътре в обема. Предимството на холограмната теория е, че вътрешните обекти изпитват гравитация, макар гравитационното взаимодействие на границата просто не съществува

За да разберем, от къде се появяват допълнителното измерение, да разгледаме една от глуонните струни на границата. Струната има дебелина, която зависи от това, доколко глуоните са размазани в пространството. Изчисленията показват, че в границата на AdS - пространството струните с различни дебелини взаимодействат една с друга толкова слабо, като че ли са разделени в пространството. С други думи, дебелината на струните може да се разглежда като пространствена координата, ос която е насочена от границата.
Така, тънката гранична струна прилича на струна, която се намира близо до границата, докато дебелата струна прилича на отдалечена от границата струна. Именно тази допълнителна координата е нужна за да се опише движението в четиримерното AdS-пространство-време! За наблюдателят в пространствено-времето граничните струни с различна дебелина изглеждат еднакво тънки, но с различни радиални позиции. Броят на цветовете на границата се определя от размера на вътрешната част на пространството (радиуса на граничната сфера). За да не отстъпва на пространство-времето по размери на видимата Вселена, на теория трябва да бъде с не по-малко от 1060 цвята.
Оказва се, че един тип глуонна верига се държи в четиримерното пространство-време, като гравитон, фундаменталната квантова частица на гравитацията. В това описание, гравитацията в четири измерения е явление, възникващо в резултат от взаимодействието на частици в тримерен свят без гравитация. Появата в теорията на гравитоните не е изненада, защото физиците знаят от 1974 г. насам, че теорията на струните по един или друг начин ще доведе до квантовата гравитация. Струните, образувани от глуони не са изключение, просто гравитацията работи в пространство с повече измерения.
Така холограмното съответствие е не просто нова възможност за създаване на квантовата теория на гравитацията. То по фундаментален начин обединява струнната теория като най-изучен подход към квантовата гравитация с теорията на кварките и глуоните, която е в основата на физиката на елементарните частици. Освен това, холограмната теория, очевидно, позволява да се състави някаква представа за точните уравнения на теорията на струните. Тя е измислена в края на 1960, за да опише силните взаимодействия, но е изоставена, когато на сцената се в появила теорията на хромодинамиката. Съответствието между струнната теория и хромодинамиката предполага, че последните усилия не са били напразни. Двете описания са различни страни на една и съща монета
Като варира хромодинамиката на границата, т.е. променя детайлите на взаимодействието на граничните частици може да се получи цял спектър от теории. По принцип на вътрешното пространство може да съдържа само гравитационната сила или гравитацията и други сили, например, електромагнитната и т.н. Все още предстои да се разработи такава гранична теория, от която то да бъде възможно да се изведе описание на вътрешното пространство, съдържащо четирите сили, управляващи нашата Вселена.



.jpg/350px-Triangles_(spherical_geometry).jpg)
Няма коментари:
Публикуване на коментар